how to find inflection point
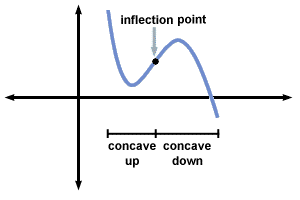
Inflection Point
![]()
An inflection point is a point where the graph of the function changes CONCAVITY (from up to down or vice versa).
It could be seen as a Switching point, which means the point that the Slope of function switch from increasing and decreasing.
e.g., the function might be still going up, but at such a point it suddenly increases slower and slower. And we call that point an inflection point.
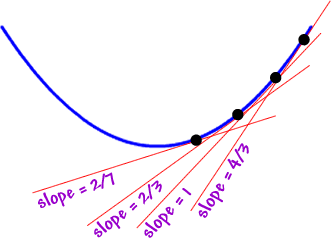
Refer to Khan academy video for more intuition rapidly: Inflection points from graphs of function & derivatives
Algebraically, we identify and express this point by the function's First DerivativeOR Second Derivative.
Example
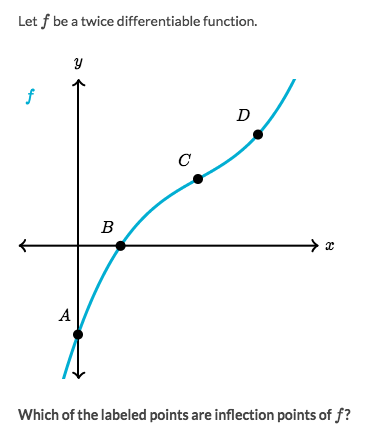
Intuitive way to solve:
- Draw a tangent line in imagination and move it on the function from left to right
- Notice the tangent line's slope, does it go faster or slower or suddenly change its pace at a point?
- We found it suddenly changed at point
c.
More definitional way to solve:
- Looking for the
parts of concavity shapes - Seems that
B-Cis a part ofConcave Down, andC-Dis a part ofConcave Up - So
Cis a SWITCHING POINT, it's ainflection point.
Example
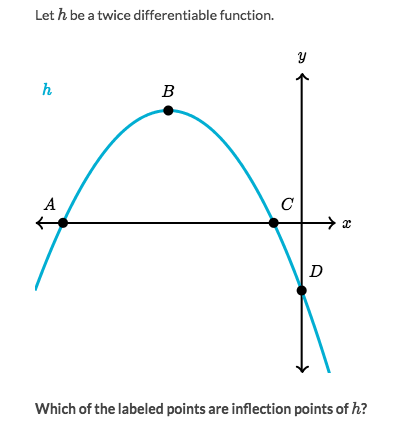
Solve:
- Looking for the
parts of concavity shapes - There's no changing of concavity shapes, there's only one shape: Concave down.
Example
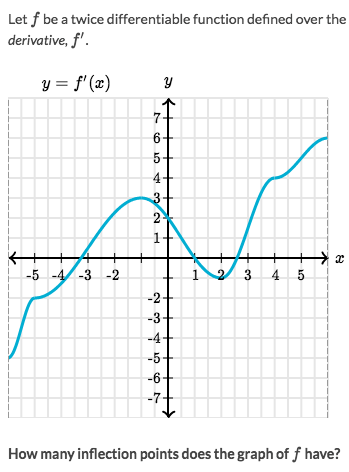
Solve:
- Notice that's the graph of
f'(x), which is the First Derivative. - Checking
Inflection pointfrom 1st Derivative is easy: just to look at the change of direction. - Obviously there're only two points changed direction: -1 & 2
Example
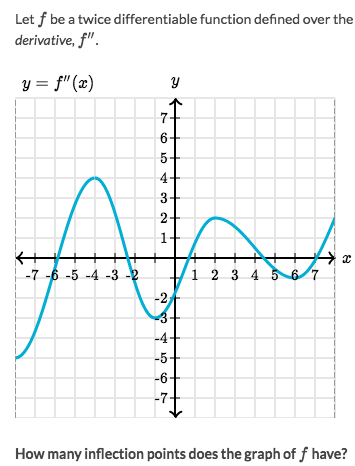
Solve:
- Mind that this is the graph of
f''(x), which is the Second derivative. - Checking
inflection pointsfrom 2nd derivative is even easier: just to look at when it changes its sign, or say crosses the X-axis. - Obviously, it crosses the X-axis 5 times. So there're 5 inflection points of
f(x).
Example: Finding Inflection points
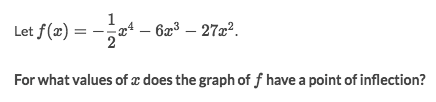
Solve:
- Function has POSSIBLE inflection points when
f''(x) = 0. - Set
f''(x) =0and solve forx, gotx=-3. - We now know the possible point, but don't know its CONCAVITY. This need to try some numbers from its both sides:
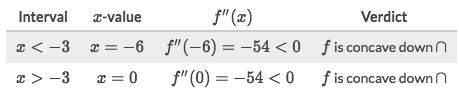
- So it didn't change the concavity at point
-3, means there's no inflection point for function.
Example: Finding Inflection points

Solve:
- Function has POSSIBLE inflection points when
f''(x) = 0. - Set
f''(x) =0and solve forx, gotx=0 or 6.
Refer to Symbolab for f''(x).)
Refer to Symbolab for f''(x)=0.
- We now know the possible point, but don't know its CONCAVITY. This need to try some numbers from its both sides:

- So it didn't change the concavity at point
0, means only6is the inflection point.
how to find inflection point
Source: https://medium.com/self-study-calculus/inflection-point-fa6fc98eca6d
Posted by: marshallzekere.blogspot.com

0 Response to "how to find inflection point"
Post a Comment